Chi
Definition
Assembly: Meta.Numerics (in Meta.Numerics.dll) Version: 4.2.0+6d77d64445f7d5d91b12e331399c4362ecb25333
public sealed class ChiSquaredDistribution : ContinuousDistributionPublic NotInheritable Class ChiSquaredDistribution
Inherits ContinuousDistributionpublic ref class ChiSquaredDistribution sealed : public ContinuousDistribution[<SealedAttribute>]
type ChiSquaredDistribution =
class
inherit ContinuousDistribution
end- Inheritance
- Object UnivariateDistribution ContinuousDistribution ChiSquaredDistribution
Remarks
A chi squared distribution is an asymmetrical distribution ranging from zero to infinity with a peak near its number of degrees of freedom ν. It is a one-parameter distribution determined entirely by the parameter ν.
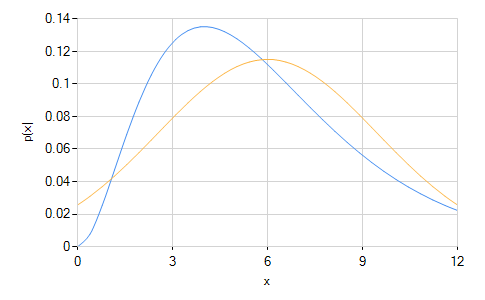
The figure above shows the χ2 distribution for ν = 6, as well as the normal distribution with equal mean and variance for reference.
The sum of the squares of ν independent standard-normal distributed variables is distributed as χ2 with ν degrees of freedom.
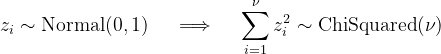
The χ2 distribution appears in least-squares fitting as the distribution of the sum-of-squared-deviations under the null hypothesis that the model explains the data. For example, the goodness-of-fit statistic returned by the model our model fitting methods (FitToFunction(FuncDouble, T, Double, Double), FitToLinearFunction(FuncT, Double), FitToLine, and others) follows a χ2 distribution.
Constructors
| ChiSquaredDistribution | Initializes a new χ2 distribution. |
Properties
| DegreesOfFreedom | Gets the number of degrees of freedom ν of the distribution. |
| ExcessKurtosis |
Gets the excess kurtosis of the distribution.
(Overrides UnivariateDistributionExcessKurtosis) |
| Mean |
Gets the mean of the distribution.
(Overrides UnivariateDistributionMean) |
| Median |
Gets the median of the distribution.
(Overrides ContinuousDistributionMedian) |
| Skewness |
Gets the skewness of the distribution.
(Overrides UnivariateDistributionSkewness) |
| StandardDeviation |
Gets the standard deviation of the distribution.
(Inherited from UnivariateDistribution) |
| Support |
Gets the interval over which the distribution is non-vanishing.
(Overrides ContinuousDistributionSupport) |
| Variance |
Gets the variance of the distribution.
(Overrides UnivariateDistributionVariance) |
Methods
| CentralMoment |
Computes a central moment of the distribution.
(Overrides ContinuousDistributionCentralMoment(Int32)) |
| Cumulant |
Computes a cumulant of the distribution.
(Overrides UnivariateDistributionCumulant(Int32)) |
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object) |
| ExpectationValue |
Computes the expectation value of the given function.
(Inherited from ContinuousDistribution) |
| GetHashCode | Serves as the default hash function. (Inherited from Object) |
| GetRandomValue |
Generates a random variate.
(Inherited from ContinuousDistribution) |
| GetRandomValues |
Generates the given number of random variates.
(Inherited from ContinuousDistribution) |
| GetType | Gets the Type of the current instance. (Inherited from Object) |
| Hazard |
Computes the hazard function.
(Inherited from ContinuousDistribution) |
| InverseLeftProbability |
Returns the point at which the cumulative distribution function attains a given value.
(Overrides ContinuousDistributionInverseLeftProbability(Double)) |
| InverseRightProbability |
Returns the point at which the right probability function attains the given value.
(Inherited from ContinuousDistribution) |
| LeftProbability |
Returns the cumulative probability to the left of (below) the given point.
(Overrides ContinuousDistributionLeftProbability(Double)) |
| ProbabilityDensity |
Returns the probability density at the given point.
(Overrides ContinuousDistributionProbabilityDensity(Double)) |
| RawMoment |
Computes a raw moment of the distribution.
(Overrides ContinuousDistributionRawMoment(Int32)) |
| RightProbability |
Returns the cumulative probability to the right of (above) the given point.
(Overrides ContinuousDistributionRightProbability(Double)) |
| ToString | Returns a string that represents the current object. (Inherited from Object) |