AdvancedMathCoulomb Method

public static SolutionPair Coulomb(
	int L,
	double eta,
	double rho
)

Public Shared Function Coulomb ( 
	L As Integer,
	eta As Double,
	rho As Double
) As SolutionPair

public:
static SolutionPair Coulomb(
	int L, 
	double eta, 
	double rho
)

static member Coulomb : 
        L : int * 
        eta : float * 
        rho : float -> SolutionPair 

Parameters

L  Int32

The angular momentum number, which must be non-negative.

eta  Double

The charge parameter, which can be positive or negative.

rho  Double

The radial distance parameter, which must be non-negative.

Return Value

The Coulomb wave functions are the radial wave functions of a non-relativistic particle in a Coulomb potential.

They satisfy the differential equation:

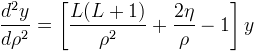
A repulsive potential is represented by η > 0, an attractive potential by η < 0.

F is oscillatory in the region beyond the classical turning point. In the quantum tunneling region inside the classical turning point, F is exponentially suppressed and vanishes at the origin, while G grows exponentially and diverges at the origin.

Many numerical libraries compute Coulomb wave functions in the quantum tunneling region using a WKB approximation, which accurately determine only the first few decimal digits; our library computes Coulomb wave functions even in this computationally difficult region to nearly full precision -- all but the last 4-5 decimal digits can be trusted.

The irregular Coulomb wave functions G_L(η,ρ) are the complementary independent solutions of the same differential equation.

Reference

Other Resources