Multivariate
Definition
Assembly: Meta.Numerics (in Meta.Numerics.dll) Version: 4.2.0+6d77d64445f7d5d91b12e331399c4362ecb25333
public MultiLinearRegressionResult LinearRegression(
int outputIndex
)Public Function LinearRegression (
outputIndex As Integer
) As MultiLinearRegressionResultpublic:
MultiLinearRegressionResult^ LinearRegression(
int outputIndex
)member LinearRegression :
outputIndex : int -> MultiLinearRegressionResult Parameters
- outputIndex Int32
- The index of the variable to be predicted.
Return Value
MultiLinearRegressionResultThe result of the regression.
Remarks
Linear regression finds the linear combination of the other variables that best predicts the output variable.
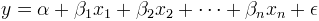
The noise term epsilon is assumed to be drawn from the same normal distribution for each data point. Note that the model makes no assumptions about the distribution of the x's; it merely asserts a particular underlying relationship between the x's and the y.
Inputs and Outputs
In the returned fit result, the indices of the parameters correspond to indices of the coefficients. The intercept parameter has the index of the output variable. Thus if a linear regression analysis is done on a 4-dimensional multivariate sample to predict variable number 2, the coefficients of variables 0, 1, and 3 will be parameters 0, 1, and 3, of the returned fit result, and the intercept will be parameter 2.
If you want to include fewer input variables in your regression, use the Columns(IReadOnlyListInt32) method to create a multivariate sample that includes only the variables you want to use in your regression.
The correlation matrix among fit parameters is also returned with the fit result, as is an F-test for the goodness of the fit. If the result of the F-test is not significant, no conclusions should be drawn from the regression coefficients.
Regression vs. Correlation
If a given coefficient is significantly positive, then a change in the value of the corresponding input variable, holding all other input variables constant, will tend to increase the output variable. Note that italicized condition means that, when there is more than one input variable, a linear regression coefficient measures something different than a linear correlation coefficient.
Suppose, for example, we take a large number of measurements of water temperature, plankton concentration, and fish density in a large number of different locations. A simple correlation analysis might indicate that fish density is positively correlated with both water temperature and plankton concentration. But a regression analysis might reveal that increasing water temperature actually decreases the fish density. This seeming paradoxical situation might occur because fish do much better with more plankton, and plankton do much better at higher temperatures, and this positive knock-on effect of temperature on fish is larger than the negative direct effect.
If we are in a situation where we can control the input variables independently -- for example we are running an aquarium -- we would certainly want to know the specific effect of one variable -- that our fishes would actually prefer us to turn down the temperature while maintaining a high plankton level -- rather than the observed effect as a variable changes along with all the others that tend to change with it. This does not mean that the correlation analysis is wrong -- higher temperatures are indeed associated with higher fish densities in our hypothetical data set. It simply means that you need to be careful to ask the right question for your purpose.
In most cases, it is indeed the specific effect of one variable when others are held constant that we seek. In a controlled experiment, the confounding effects of other variables are removed by the experimental design, either by random assignment or specific controls. In an observational experiment, though, confounding effects can be, and often are, large, and correlation analysis is not sufficient. It is worthwhile keeping this in find in politically charged debates in which easily observed correlations are likely to be bandied about as evidence, while a more difficult regression analysis that would actually be required to support an assertion is left undone.
Cavets
It can occur that two theoretically independent variables are so closely correlated in the observational data that a regression analysis cannot reliably tease out the independent effect of each. In that case, a fit using only one of the variables will be as good or nearly as good as a fit using both, and the covariance between their corresponding linear regression coefficients will be large. In a situation like this, you should be wary of drawing any conclusions about their separate effects.
It can also occur that an input variable or a set of input variables is indeed good predictor of an output variable, but via a complex and non-linear relationship that a linear regression analysis will completely miss.
Exceptions
| ArgumentOutOfRangeException | outputIndex is outside the range of allowed indexes. |
| InsufficientDataException | There are fewer entries than the dimension of the multivariate sample. |
| DivideByZeroException | The curvature matrix is singular, indicating that the data is independent of one or more parameters, or that two or more parameters are linearly dependent. |