Normal
Definition
Assembly: Meta.Numerics (in Meta.Numerics.dll) Version: 4.2.0+6d77d64445f7d5d91b12e331399c4362ecb25333
public sealed class NormalDistribution : ContinuousDistributionPublic NotInheritable Class NormalDistribution
Inherits ContinuousDistributionpublic ref class NormalDistribution sealed : public ContinuousDistribution[<SealedAttribute>]
type NormalDistribution =
class
inherit ContinuousDistribution
end- Inheritance
- Object UnivariateDistribution ContinuousDistribution NormalDistribution
Remarks
A normal distribution is a bell-shaped curve centered at its mean and falling off symmetrically on each side. It is a two-parameter distribution determined by giving its mean and standard deviation, i.e. its center and width. Its range is the entire real number line, but the tails, i.e. points more than a few standard deviations from the means, fall off extremely rapidly.
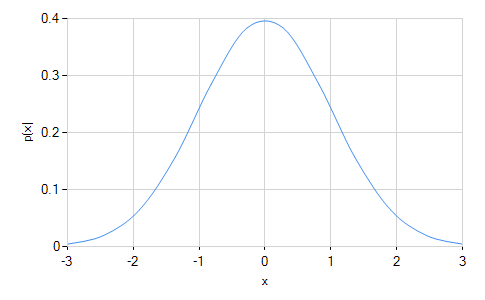
A normal distribution with mean zero and standard deviation one is called a standard normal distribution. Any normal distribution can be converted to a standard normal distribution by re-parameterizing the data in terms of "standard deviations from the mean", i.e. z = (x - μ) / σ.
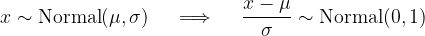
Normal distribution appear in many contexts. In practical work, the normal distribution is often used as a crude model for the distribution of any continuous parameter that tends to cluster near its average, for example human height and weight. In more refined theoretical work, the normal distribution often emerges as a limiting distribution. For example, it can be shown that, if a large number of errors affect a measurement, then for nearly any underlying distribution of error terms, the distribution of total error tends toward a normal distribution.
The normal distribution is often called a Gaussian, after the mathematician Friedrich Gauss.
Constructors
| NormalDistribution | Initializes a new standard normal distribution. |
| NormalDistribution(Double, Double) | Initializes a new normal distribution with the given mean and standard deviation. |
Properties
| ExcessKurtosis |
Gets the excess kurtosis of the distribution.
(Overrides UnivariateDistributionExcessKurtosis) |
| Mean |
Gets the mean of the distribution.
(Overrides UnivariateDistributionMean) |
| Median |
Gets the median of the distribution.
(Overrides ContinuousDistributionMedian) |
| Skewness |
Gets the skewness of the distribution.
(Overrides UnivariateDistributionSkewness) |
| StandardDeviation |
Gets the standard deviation of the distribution.
(Overrides UnivariateDistributionStandardDeviation) |
| Support |
Gets the interval over which the distribution is non-vanishing.
(Inherited from ContinuousDistribution) |
| Variance |
Gets the variance of the distribution.
(Inherited from UnivariateDistribution) |
Methods
| CentralMoment |
Computes a central moment of the distribution.
(Overrides ContinuousDistributionCentralMoment(Int32)) |
| Cumulant |
Computes a cumulant of the distribution.
(Overrides UnivariateDistributionCumulant(Int32)) |
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object) |
| ExpectationValue |
Computes the expectation value of the given function.
(Inherited from ContinuousDistribution) |
| FitToSample | Computes the normal distribution that best fits the given sample. |
| GetHashCode | Serves as the default hash function. (Inherited from Object) |
| GetRandomValue |
Generates a random variate.
(Overrides ContinuousDistributionGetRandomValue(Random)) |
| GetRandomValues |
Generates the given number of random variates.
(Inherited from ContinuousDistribution) |
| GetType | Gets the Type of the current instance. (Inherited from Object) |
| Hazard |
Computes the hazard function.
(Inherited from ContinuousDistribution) |
| InverseLeftProbability |
Returns the point at which the cumulative distribution function attains a given value.
(Overrides ContinuousDistributionInverseLeftProbability(Double)) |
| InverseRightProbability |
Returns the point at which the right probability function attains the given value.
(Overrides ContinuousDistributionInverseRightProbability(Double)) |
| LeftProbability |
Returns the cumulative probability to the left of (below) the given point.
(Overrides ContinuousDistributionLeftProbability(Double)) |
| ProbabilityDensity |
Returns the probability density at the given point.
(Overrides ContinuousDistributionProbabilityDensity(Double)) |
| RawMoment |
Computes a raw moment of the distribution.
(Overrides ContinuousDistributionRawMoment(Int32)) |
| RightProbability |
Returns the cumulative probability to the right of (above) the given point.
(Overrides ContinuousDistributionRightProbability(Double)) |
| ToString | Returns a string that represents the current object. (Inherited from Object) |