Represents the Cholesky Decomposition of a symmetric, positive definite matrix.
Declaration Syntax| C# | Visual Basic | Visual C++ | F# |
public sealed class CholeskyDecomposition
Public NotInheritable Class CholeskyDecomposition
public ref class CholeskyDecomposition sealed
[<SealedAttribute>] type CholeskyDecomposition = class end
Members| All Members | Methods | Properties | |||
| Icon | Member | Description |
|---|---|---|
 | Determinant()()()() |
Computes the determinant of the original matrix.
|
 | Dimension |
Gets the dimension of the system.
|
| Equals(Object) | (Inherited from Object.) |
 | Finalize()()()() | Allows an Object to attempt to free resources and perform other cleanup operations before the Object is reclaimed by garbage collection. (Inherited from Object.) |
| GetHashCode()()()() | Serves as a hash function for a particular type. (Inherited from Object.) |
| GetType()()()() | Gets the Type of the current instance. (Inherited from Object.) |
| Inverse()()()() |
Computes the inverse of the original matrix.
|
| MemberwiseClone()()()() | Creates a shallow copy of the current Object. (Inherited from Object.) |
| Solve(IList<(Of <<'(Double>)>>)) |
Computes the solution vector that, when multiplied by the original matrix, produces the given left-hand side vector.
|
| SquareRootMatrix()()()() |
Returns the Cholesky square root matrix.
|
| ToString()()()() | (Inherited from Object.) |
RemarksA Cholesky decomposition represents a matrix as the product of a lower-left triangular matrix and its transpose. For example:
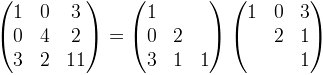
The Choleksy decomposition of a symmetric, positive definite matrix can be obtained using the CholeskyDecomposition()()()() method of the SymmetricMatrix class.
ExamplesHere is an example that uses a Cholesky decomposition to solve a linear algebra problem.
CopyC#// Solve Ax = b via Cholesky decomposition CholeskyDecomposition CD = A.CholsekyDecomposition(); ColumnVector b = new ColumnVector(1.0, 2.0, 3.0); ColumnVector x CD.Solve(b);
Inheritance Hierarchy| Object | |
 | CholeskyDecomposition |
See Also