Singular
Definition
Assembly: Meta.Numerics (in Meta.Numerics.dll) Version: 4.2.0+6d77d64445f7d5d91b12e331399c4362ecb25333
public sealed class SingularValueDecompositionPublic NotInheritable Class SingularValueDecompositionpublic ref class SingularValueDecomposition sealed[<SealedAttribute>]
type SingularValueDecomposition = class end- Inheritance
- Object SingularValueDecomposition
Remarks
The singular value decomposition of a matrix represents it as a product of a left orthogonal matrix U, a quasi-diagonal Σ matrix, and a right orthogonal matrix V.
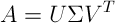
Any rectangular matrix has an SVD decomposition. The matrix need not be square. If square, it need not be invertible. The dimensions of the decomposition factors are illustrated in the following diagram.
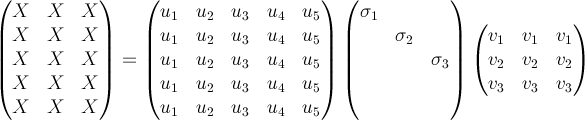
The elements of the Σ are called the singular values of the original matrix.
Viewing A as a linear operator, the rows of VT (columns of V) form an orthonormal basis for the domain of the operator, while the columns of U form an orthonormal basis for the range of the operator. These rows and columns are called, respectively, the right and left singular vectors of the matrix.
The right singular vectors corresponding to zero singular values span the null-space of A, that is the set of all x for which Ax = 0. The left singular vectors corresponding to non-zero singular values span the range of A, that is the space into which all Ax fall; the left singular vectors corresponding to zero singular values span the complementary space into which no Ax fall. The total number of non-zero singular values is the rank of A.
The SVD can be used to approximate the action of a high-dimensional matrix operator by a lower-rank one. By keeping only the largest singular values and setting the remaining ones to zero, one obtains a operator that can applied with fewer operations and approximates the properties of the original operator.
Notice that elements in the last columns of U do not contribute to A since they will be multiplied with elements of zero rows of Σ. Many applications use a "thin" or "reduced" form of the SVD, in which the last columns of U and the last rows of Σ are omitted; this makes U not square (and therefore not orthogonal) and Σ square (and diagonal). Since the remaining elements are the same, you can obtain the thin SVD from this object by simply ignoring the irrelevant elements.
Use the SingularValueDecomposition of the RectangularMatrix class to obtain the SVD of an rectangular matrix, or the corresponding SingularValueDecomposition method of the SquareMatrix class to obtain the SVD of a square matrix.
Properties
| ColumnCount | Gets the number of columns in the original matrix. |
| ConditionNumber | Gets the condition number of the matrix. |
| Contributors | Gets a collection of all the terms contributing to the singular value decomposition. |
| Dimension | Gets the number of singular values. |
| LeftTransformMatrix | Gets the left transform matrix. |
| Rank | Computes the rank of the original matrix. |
| RightTransformMatrix | Gets the right transform matrix. |
| RowCount | Gets the number of rows in the original matrix. |
| Tolerance | Gets or sets the tolerance with which singular values are distinguished from zero. |
Methods
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object) |
| GetHashCode | Serves as the default hash function. (Inherited from Object) |
| GetType | Gets the Type of the current instance. (Inherited from Object) |
| Solve | Solves the system of equations Ax = b, where A is the original, square matrix. |
| ToString | Returns a string that represents the current object. (Inherited from Object) |