AdvancedIntegerMathBinomialCoefficient Method

public static double BinomialCoefficient(
	int n,
	int m
)

Public Shared Function BinomialCoefficient ( 
	n As Integer,
	m As Integer
) As Double

public:
static double BinomialCoefficient(
	int n, 
	int m
)

static member BinomialCoefficient : 
        n : int * 
        m : int -> float 

Parameters

n

Type: SystemInt32
The upper argument, which must be non-negative.

m

Type: SystemInt32
The lower argument, which must be non-negative and less than or equal to n.

Return Value

The binomial coefficient C(n, m) is the coefficient of x^m in the expansion of (1+x)ⁿ:

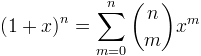
Writing n over m in parenthesis, as in the expression above, is by far the most common notation for binomial coefficients, even though it is difficult to write inline.

C(n,m) can also be given a combinatoric interpretation as the total number of ways to pick m items from a set of n distinct items. For this reason, it is often read as "n choose m".

For example C(4,2) = 6. This can be seen by expanding (1+x)⁴ = 1 + 4 x + 6 x² + 4 x³ + x⁴ and noting that the coefficient of the x² term is 6. It can also be seen by considering the four-member set (abcd) and noting that there are 6 possible two-member subests: (ab), (ac), (ad), (bc), (bd), (cd).

Pascal's triangle is a classic graphical representation of binomial coefficients:

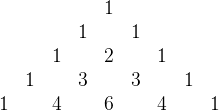
The nth row of Pascal's triangle consists of the binomial coefficients C(n, 0) to C(n, n). Because of the triangular arrangement, the identity C(n+1, m) = C(n, m-1) + C(n, m) corresponds to a rule that each entry is the sum of the two neighboring entries from the row above. This rule makes it easy to generate additional rows. (Proceeding in this fashion from C(0, 0) to the desired C(n, m) would be a very inefficient algorithm for generating C(n, m). It is not how this method is implemented.) Pascal's triangle exhibits many other fascinating patterns that arise from various binomial coefficient identities.

If you need multiple, sequential binomial coefficients from a row of Pascal's triangle, that is multiple C(n, m) with the same n and increasing m, it is much more efficient to use BinomialCoefficients(Int32), which generates the coefficients iteratively, than to call this method independently for each one.

Reference

Other Resources