Gamma Method (x)

Computes the Gamma function.

Declaration Syntax

Visual Basic

Visual C++

public static double Gamma(
	double x
)

Public Shared Function Gamma ( _
	x As Double _
) As Double

public:
static double Gamma(
	double x
)

static member Gamma : 
        x:float -> float

Parameters

x (Double): The argument.

Return Value

The value of Γ(x).

Remarks

The Gamma function is a generalization of the factorial (see Factorial(Int32)) to arbitrary real values.

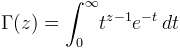
For positive integer arguments, this integral evaluates to Γ(n+1)=n!, but it can also be evaluated for non-integer z.

Because Γ(x) grows beyond the largest value that can be represented by a Double at quite moderate values of x, you may find it useful to work with the LogGamma(Double) method, which returns ln(Γ(x)).

To evaluate the Gamma function for a complex argument, use Gamma(Complex).